Two mathematical parameters are commonly used to define the growth of a bacterial culture:
- growth rate constant
- mean generation time
Note that both of these factors only relate to the exponential phase of growth, which must be determined empirically (from the graph).
Calculate the growth rate constant:
During the exponential (or logarathmic) growth phase, a bacterial culture mimics a first-order chemical reaction, i.e. the rate of increase of cells is proportional to the number of bacteria present at that time. The constant of proportionality, µ, is an index of the growth rate and is called the growth rate constant:
Rate of increase of cells = µ x number of cells
The value of µ can be determined from the following equation:
ln Nt - ln N0 = µ(t - t0)
in other words:
the natural log of the number of cells at time t minus the natural log of the number of cells at time zero (t0) equals the growth rate constant multiplied by the time interval.
For most purposes, it is easier to use log10 values rather than natural logs, so the above equation can be converted as follows:
log10 N - log10 N0 = (µ/2.303) (t -
t0)
or alternatively:
µ = ( (log10 N - log10 N0) 2.303) /
(t - t0)
By measuring the increase in the number of cells during a certain time period, the growth rate constant (µ) can be calculated. In the experiment you have just done:
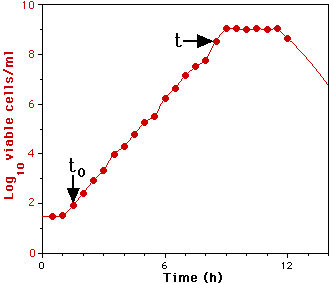 |
t0 = 1.5h:
N = 8.4x101,
log10 N = 1.92
t = 8.5h:
N = 3.39x108,
log10 N = 8.53
|
Therefore in this case:
µ = ( (log10 N - log10 N0) 2.303) / (t - t0)
= ( (8.53 - 1.92) 2.303) / (8.5 - 1.5)
= (6.61 x 2.303) / 7
= 15.22 / 7
= 2.18 hour-1
Now calculate the mean generation time:


DISCLAIMER © AJC
2002.